Body Mass Index: Introduction and History to BMI

Body Mass Index (BMI) is a measure of relative mass based on ones height and weight. Originally named the Quételet Index after Belgian astronomer, mathematician, statistician and sociologist Adolphe Quételet.
BMI is defined as one’s body mass divided by the square of their height in units of kg/m2 as shown on the BMI Formula page.
Assuming that someone were to calculate their BMI using the standard metric formula and obtained a BMI equivalent to 26.41 kg/m2, what would this tell us about the individual’s relative mass and height? We would need to refer to our BMI Classification.
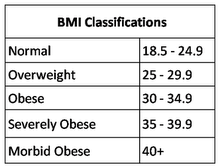
BMI Classification (International Standard)
As we can see here, a BMI of 26.41 would fall into the Overweight category. The following graph will show the varying BMI values depending on height and mass. Notice that people with differing height and mass may have the same BMI.

The portions with the same colour represent a classification or category. For example all the red areas are considered obese which means over a BMI of 30.
History and Usage
Adolphe Quételet devised the Quételet Index between 1830 and 1850 during the course of ‘social physics.’ His purpose was to obtain a relationship to describe the standard proportions of the human body using the ratio of mass and height in the average adult. Throughout Quételet’s research, he found that mass varied not in direct proportion with height but rather more closely to the square of the height.
What does this mean exactly?
An easy way to understand this would be with a simple but effective example:
Example
Let’s say that we have an individual that is 100 kg with a height of 2 m. If we were to increase the height of this individual by 10%,
a) what would his mass be if we used a direct proportion of mass and height?
b) what would his mass be if we used the BMI relationship (i.e. square of the height) between mass and height?
Solution
a) Since mass and height are related with a direct proportion, we would simply increase the mass with the same relative amount that height increased. In this case we would increase the mass by 10% since height increased by 10%. Therefore our individual would weigh 110 kg with a height of 2.2 m.
a) Using the equation BMI = mass/height^2, we can see that the relationship is not a direct proportion. What we would do set up an equation to solve for the new mass:
mass(initial)/(height(initial))^2 = mass(new)/((height(new))^2
All of the variables are known except for mass(new). So now we plug in the values and solve for the unknown.
The mass(new) works out to be 121 kg
Conclusion
Throughout his research, Quételet noticed that through multiple samples, the relationship between mass and height is not directly proportional at all and rather is much more closely related to his Index. Although the true proportion of average mass among adults is not exactly related to the square of the height, it is very close and is much more accurate than direct proportion.
History and Usage Continued
The Quételet Index was not widely used at first until post WW2 when the relationship between weight and cardiovascular disease become a subject of study –Eknoyan (2007). It was known as the Quételet Index until the term “Body Mass Index” was used by Ancel Keys et al in his 1972 paper entitled: “Indices of relative weight and obesity.” In his paper, he concluded that BMI was the best proxy for body fat percentage among ratios of weight and height.
BMI is widely used as a simple method to assess an individual’s body weight relative to his height to have a comparison to what is labeled as ‘normal.’
There is a strong debate to the thresholds of the BMI classifications. For example, what is considered underweight, overweight, normal and obese is a hard thing to pin point. Furthermore, there are some limitations to BMI that should be addressed also:
1) Scaling up: Larger Individuals have larger BMI’s even if there is an exact same proportions
2) Individuals with high muscle mass will have larger BMI values
3) There is a variation depending on your age, gender and population



